Elzear - 🗳 ranked voting systems

The spoiler effect in elections can be frustrating. I wish my preferred candidates would not “steal” votes from each other. And I wish I would never have to lie about my preferences for my vote to count.

Elections are unfair.
🗳️ 😠 📊 😤
How to prevent dishonesty as a winning strategy?

Let's discover several election systems which better reflect the voters' opinions. This article partially answers the question: how to fairly gather the preferences of a group of voters to select a winner?No information from this post is new. Most of the content is heavily inspired from the following sources:

the Wikipedia article on electoral systems,
the presentation of Practical Voting Rules and other online documents from Dr Felix Brandt,
YouTube videos: Politics In The Animal Kingdom from CGP Grey and La démocratie sous l'angle de la théorie des jeux (in French) by Science4All,

This blog post is a simple introduction to ranked voting systems and a presentation of a few voting methods. Also this is not an academic paper, I tried my best to compile information but there is a good chance that errors slipped into this post.

Discover
ranked 🥇🥈🥉
election systems

The problem space

xkcd voting referendum (https://xkcd.com/2225/) — xkcd: Voting Referendum

In real-world elections, we are generally unable to express our entire preference order. Most of the time, we are only able to select one single candidate with our ballot. This leads us to lie about our preferences, for example when a vote would be “wasted” on an underdog (this is the spoiler effect). Elections could be fairer if voters would be able to indicate their full preference order! It could then be taken into account and better reflect people's opinions. Also, entering all preferences in one ballot allows us to compute elections of multiple rounds at once, without having to force the voters to cast multiple ballots for the same election.There are 2 main ways to record voters' opinion:

ranked voting: each voter can submit an order of preference between the candidates
cardinal voting: each voter grades the candidates on a scale. For example rating all candidates between 0 and 5.

Number the boxes in order of your choice

4 Hayden Kelly
Lesley Poole
4 Marley Bennett
3 Lesley Mills
Erin Fraser
1 Brett Nielsen
4 Noel Curry
2 Vic Levy
Tanner Fleming
2 Glen Hoffman

Example of a ranked ballot. The preferred candidate of this voter is Brett Nielsen

Even though cardinal voting has many supporters, I dislike it for enabling voters to vote tactically: one can benefit from lying. For example, by only giving extreme grades, a voter can have more impact than the others. Therefore this article will only focus on ranked voting.

Voters can rank alternatives in a sequence, possibly with ties. Ballots contain ranked (not rated!) candidates. The ballots accept ties: if voters are indifferent between two candidates, they can put them in the same rank in their ballots.
The goal of the vote is to compute a hierarchy among the alternatives along with a winner. This means the vote can select options like a restaurant for the evening, a president… Proportional representation, like electing a parliament, is not a subject of this article.
For the sake of simplicity, ties and tie-breakers are ignored in this article. The examples were chosen not to result in tied situations.

5 simple voting systems

Let's consider an election in the animal world (copying CGP Grey's videos) with a particular voting scenario invented by Michel Balinski, a mathematician, economist and political scientist.This is a virtual election with 100 voters and 5 candidates:

🐸 Frog

🐷 Pig

🦁 Lion

🐻 Bear

and

🐭 Mouse

The voters can be gathered in 6 groups, each having the same preference order. The preferences of all the voters are represented in this array (which must be read as “33 voters (first column) rank Frog first, then Pig, then Lion, then Bear and finally Mouse is their least favourite; 16 voters (second column) rank Pig first, then Bear, then Lion; etc.”):

33	16	3	8	18	22
🐸 Frog	🐷 Pig	🦁 Lion	🦁 Lion	🐻 Bear	🐭 Mouse
🐷 Pig	🐻 Bear	🐻 Bear	🐭 Mouse	🐭 Mouse	🦁 Lion
🦁 Lion	🦁 Lion	🐷 Pig	🐷 Pig	🦁 Lion	🐷 Pig
🐻 Bear	🐭 Mouse	🐸 Frog	🐻 Bear	🐷 Pig	🐻 Bear
🐭 Mouse	🐸 Frog	🐭 Mouse	🐸 Frog	🐸 Frog	🐸 Frog

We can compare some voting systems using this preference profile as an input.

First past the post

Probably the most basic voting method. Only the first choice of each voter matters and we simply count the votes. It is used in elections in many countries (the USA, the UK, Canada...).With the voting system first past the post: Frog gets 33 votes, which is better than any other candidates.

🐸 Frog

wins.This result can feel unfair because voters' preferences are hardly taken into account. Frog won because it is ranked first by the biggest group (33%), but it is also ranked last by the majority of voters (56%)! That 56% (who ranked Frog last) could potentially come together before the start of the vote and agree on their preferred candidate — which would be Mouse — to prevent Frog from being elected.

Contingent vote / Two-round run-off

With these methods, if no candidate receives 50% of the votes in the first round, a second round of voting is held with only the top two candidates.The Contingent vote lets voters cast their preference order at once and the winner can be computed without needing another vote.In two-round run-off elections, voters are only asked about their preferred candidate. They have to vote again in the second round. 47 countries (Finland, France, Russia, Turkey...) use this system for their presidential elections.A candidate ranked last by more than 50% of the voters cannot be elected by these methods.With the voting system two-round run-off: Frog and Mouse compete in the second round and

🐭 Mouse

wins with 64% of the votes.But Mouse is still the second most disliked candidate: if we remove the most disliked candidate (Frog), we are left with 52% of the voters ranking Mouse last! Those voters can understandably be unsatisfied and ask for a different system to be used.

Instant Run-off

Counting only the first choices of the voters, the candidate with the fewest votes is eliminated. The election repeats until there is a winner. It is used for example to elect members of the Australian House of Representatives, the president of India and the president of Ireland.Lion is eliminated first, then Pig, then Mouse, then Frog. The final winner of the instant run-off vote is

🐻 Bear

.Knowing the outcome of that vote, some groups could have changed their ballots to prevent Bear's election. For example, the 33%-group could decide to rank Pig first, and provoke the election of Pig instead of Bear!Coombs' rule is a similar voting method where the candidate ranked last by most voters gets eliminated each round. This rule would elect Pig.

Borda's rule

For each voter, every candidate is given points corresponding to their rank in the voter's preferences. In our case: the first position gets 5 points, the second position gets 4 points… It is currently used to elect members of the Parliament of Nauru and two ethnic minority members of the National Assembly of Slovenia.With Borda's rule:

🐷 Pig

wins with 347 points, and Lion is second with 344 points.If the voters knew that the race would be so close between Pig and Lion, they probably would have tried to influence the election by ranking them as the first or the last in their ballots. Since 51% of the voters prefer Lion to Pig, they can change the outcome of the election. This kind of phenomenon often leads political systems to be bipartisan.

Copeland's method

Finally, someone found the perfect voting system for this election! Copeland's method considers all duels between the candidates and counts the number of victories, similarly to a tournament.

Wins count:

🐸 Frog: 0

🐷 Pig: 3

🦁 Lion: 4

🐻 Bear: 2

🐭 Mouse: 1

Using Copeland's method:

🦁 Lion

wins. In fact, Lion wins all the duels, this is called a Condorcet winner. Interestingly, this candidate was never selected as a winner by the other real-world voting methods even though it wins all duels! The voters of this election are finally happy thanks to Copeland's method: the winner of all duels wins the election, everything is perfectly logical.Did you notice? The 5 voting systems gave 5 different winners while the electors did not change their preferences! 🤯

Just pick the candidate winning all duels?! — Condorcet winners and Condorcet paradox

Preferences graph helps to visualize duels

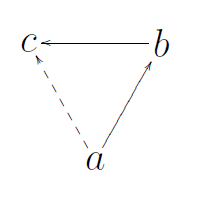
To visualize the duels, it is helpful to simplify the representation of the input by using a graph instead of an array of preferences.The preference of the first group of voters (33%: Frog → Pig → Lion → Bear → Mouse) can be represented like this:Adding the preferences of all the voters, we get the full graph:Did I say simplify? 😬
We can still combine opposed edges, which makes it way more readable:

🦁 Lion

, with all edges going outwards, is the Condorcet winner (winner of all duels).

Condorcet paradox

After seeing Copeland's method, you may think “Just pick the candidate that wins all duels!”. It would be great if this was always possible, but unfortunately, there are situations where no candidate wins all duels and a cycle appears.

Using a ranked voting method, each voter submits a ballot with a transitive preference of the candidates. Given that voters submit a clear hierarchical order, why can't voting systems simply agree on a winner? Why is it so hard to aggregate voters' preference orders? Can't Copeland's method always be used?With 3 candidates or more, problems may start to arise since some collective preferences can be cyclic. Here is an example of a vote for the best food. 15 voters are deciding between the following candidates:

🌯 Burrito

🍔 Burger

🍕 Pizza

🍪 Cookie

Number of voters	Preference order
6	🌯 Burrito > 🍕 Pizza > 🍔 Burger > 🍪 Cookie
4	🍕 Pizza > 🍪 Cookie > 🍔 Burger > 🌯 Burrito
4	🍪 Cookie > 🍔 Burger > 🍕 Pizza > 🌯 Burrito
1	🌯 Burrito > 🍔 Burger > 🍕 Pizza > 🍪 Cookie

This preference profile can also be represented in the below form, as we saw previously:

	6	4	4	1
🥇	🌯 Burrito	🍕 Pizza	🍪 Cookie	🌯 Burrito
🥈	🍔 Burger	🍪 Cookie	🍔 Burger	🍔 Burger
🥉	🍕 Pizza	🍔 Burger	🍕 Pizza	🍕 Pizza
💩	🍪 Cookie	🌯 Burrito	🌯 Burrito	🍪 Cookie

Or as an array of duels:

vs.	🌯 Burrito	🍔 Burger	🍕 Pizza	🍪 Cookie
🌯 Burrito		-1	-1	-1
🍔 Burger	1		7	-1
🍕 Pizza	1	-7		7
🍪 Cookie	1	1	-7

Or as a graph of duels:It shows that no alternative wins all pairwise duels: There is a cycle between

🍔 Burger

🍕 Pizza

and

🍪 Cookie

, this vote has no Condorcet winner. In this kind of scenario, it is not obvious who should win.

4 Condorcet voting systems

The Copeland voting system, which we saw above, validates the Condorcet criteria. Some more complex voting systems can validate the Condorcet criterion and also score better on other criteria (see below).The previous election example was too simple: there was a Condorcet winner (Lion) which deserved to win, and it would be selected as a winner by all those Condorcet-methods. With a new fictional election in the animal kingdom, we can compare our new voting systems.Read the following table as “2 voters rank Lion first, then Pig and Bear (tied), then Frog and then Mouse as their least favourite; 3 voters rank Mouse first, then Bear, etc.”

2	3	5	7	8	9	10	10	14
🦁	🐭	🐻	🐻	🐷	🦁	🐷 - 🐸	🐻	🐭
🐷 - 🐻	🐻	🐭	🐷 - 🐭	🦁	🐻	🐭 - 🦁	🐭	🐸
🐸	🐷	🦁	🦁	🐸	🐸	🐻	🐸	🐷
🐭	🐸	🐷	🐸	🐻	🐷 - 🐭		🦁	🦁
	🦁	🐸		🐭			🐷	🐻

This array is not the best way to visualize votes for the Condorcet methods. Pairwise preferences (duels between each candidate) are the important data here. The table of duels (see the array in Minimax method) or the graph of duels (see Ranked pairs method) are the proper ways to visualize the voting data.This election is very messy. It does not have a Condorcet winner, preferences of the group form many cycles. Note that those votes are carefully chosen to show different results depending on the voting system. The results for each voting system would normally not differ this much.

Minimax

Select the candidate for which the biggest pairwise defeat is smaller than the biggest pairwise defeat of all other candidates.

vs.	🐷 Pig	🦁 Lion	🐸 Frog	🐻 Bear	🐭 Mouse
🐷 Pig		8	-3	2	-7
🦁 Lion	-8		6	-4	10
🐸 Frog	3	-6		-1	9
🐻 Bear	-2	4	1		-5
🐭 Mouse	7	-10	-9	5

Bear's strongest defeat is -5 (against Mouse). All other candidates face stronger strongest defeats.

🐻 Bear

wins the vote with the Minimax method.A Condorcet loser (a candidate losing all duels) may be selected as the winner by the Minimax method, which is probably not ideal.

Ranked Pairs

To compute the winner with Ranked Pairs methods, iterate through the edges of the graphs by descending strength and accept them in a graph as long as they do not create cycles. The resulting graph is acyclic and its root is the election winner.The generated acyclic graph has the order “🐷 → 🦁 → 🐸 → 🐭 → 🐻”.

🐷 Pig

wins the ranked pairs vote.

Schulze method

For each pair of candidates, find the path from one to the other with the strongest weakest link (the path using the edges which are as strong as possible). The candidate which has stronger paths outwards than paths inwards is the winner. In the following example, click on the array cells to highlight the paths of the duels.Frog has paths to all opponents that are stronger than the paths from the opponents to Frog. Therefore,

🐸 Frog

is the winner with the Schulze method."Schulze method users included Debian, Gentoo, Topcoder, Wikimedia, KDE, the Pirate Party of Sweden, and the Pirate Party of Germany" (Wikipedia).

Kemeny rule

Find an order that contradicts as few preferences as possible. This method can take very long to compute if there are many candidates because there are n! possibilities, with n being the number of candidates. For 5 candidates, there are already 120 possibilities to check (of course there are certainly better ways to greatly reduce the search space).The order “🦁 → 🐸 → 🐭 → 🐷 → 🐻” is the one that contradicts edges the least (by the sum of weights): 3 edges with a total value of 13 points have a direction opposite to that order. The top candidate of this order,

🦁 Lion

, wins the election with Kemeny's rule.

Randomization: the solution against strategic voting

All the methods listed above share the same flaw: they are all vulnerable to strategic voting. Meaning that there can be situations in which a voter could lie about his or her preferences and end up with a preferred outcome, that is unfair.Vulnerability to strategic voting is probably the worst flaw of voting systems. This is a problem of all real-world methods. By introducing randomness to the process, some resistance to tactical voting can be built.

Random ballot

Also known as random dictator, this voting system simply consists of picking a ballot at random, which determines the winner. Despite its simplicity, this method has the advantage of being resistant to tactical voting.Using the preference profiles from above the generated lottery is as follows:Out of the 68 voters, 22 ranked Bear first. Which means Bear gets a 32% chance of winning (22 / 68).While it is great to be strategy-resistant: the random ballot voting system has many flaws. For example, an unfortunate roll of dice could give the win to a heavily disliked candidate. And, more importantly, this method fails the Condorcet criterion.

Maximal lotteries

The maximal lotteries method consists in computing the Nash equilibrium corresponding to the matrix of duels. Then assigning probabilities to candidates proportionally to their score in the Nash equilibrium.With the duel matrix A, we must find a vector v such asv A ≥ 0 (meaning all values of the product are positive).In our example the matrix A is:

And the vector v which verifiesv A ≥ 0:

Which produces this lottery:In real-life elections, having such Condorcet-cycles is unlikely. Which means that most candidates would normally be given a probability of 0. Unfortunately, maximal lotteries are not resistant to tactical voting.

Randomized Condorcet voting

This method is very similar to maximal lotteries, and is more resistant to tactical voting. "When a Condorcet winner exists, it must be selected and no voter has incentives to misreport his preferences" (Strategy-proofness of the randomized Condorcet voting system).The only difference is that the randomized Condorcet voting system uses the matrix of duels with values of 1 or -1.

a few examples showing Randomized Condorcet probabilities in different graphs

In this very particular case, the solution is the vector( 1 1 1 1 1 ) and the corresponding lottery gives 20% chances to each of the 5 candidates.This method ignores the strength of the victories. Also, the probabilities change in a non-continuous fashion: small changes in the votes don't change the probabilities until they change the winner of a duel, then it alters the probabilities drastically and suddenly. Those traits may be a disadvantage.

Yet another voting application

I made a small web app allowing the use of a few different voting systems. You can create polls, add candidates and rank them according to your preferences. Next time you have to make a group decision, you may want to use this tool!

Create a poll on elzear.de!🗳 Happy voting! 🗳

It is still under development, so there are some bugs here and there. The code source for the different voting systems is available in the npm votes library (GitHub). PRs, bug reports and any feedback are very welcome!There is also an UI tool allowing to see the results for several voting system: rank-votes.vercel.app.

Some fairness criteria

To compare the voting systems that were presented, there is a list of criteria that can be used.

Condorcet: If one candidate wins all duels against others, then that candidate must win the election. W

Majority: If one candidate is ranked first by more than 50% of voters, then that candidate must win. W

Monotonicity: By redoing an election with everything unchanged but the preferences of 1 voter, which now rank 1 candidate higher in the list, then the election result should not place this candidate lower than before. In other words, an individual should not be able to hurt an option by ranking it higher. W

Pareto efficiency: If every voter prefers alternative X over alternative Y, then the system prefers X over Y. W

Independence of irrelevant alternatives (IIA): Assuming voter preferences regarding other candidates are unchanged, the winner never changes if a non-winning candidate is added or removed. W

Local Independence of irrelevant alternatives (LIIA): Assuming voter preferences regarding other candidates are unchanged, removing the candidate at the first place or the last place should not change the order of the remaining candidates. W

Non-dictatorship: The result of the voting cannot be determined by the preference of one voter without taking the other votes into account. W

Strategy proof: Lying about preferences never leads to a preferred outcome W

Why can't we fulfil all the criteria?

Arrow's impossibility theorem

A mathematician, Dr Kenneth Arrow, showed that no rank-order deterministic voting system could fulfil those 3 criteria: non-dictatorship, Pareto efficiency, and independence of irrelevant alternatives. The theorem is Arrow's impossibility theorem. This means that we have to make some compromises by giving up on some criteria.

Gibbard–Satterthwaite theorem

Another theorem is easier to understand. It goes like this (paraphrased from Wikipedia):

In deterministic ordinal electoral systems (aka ranked voting) that choose a single winner, for every voting rule, one of the following three things must hold:

The rule is dictatorial, i.e. there exists a distinguished voter who can choose the winner; or

The rule limits the possible outcomes to two alternatives only; or

The rule is susceptible to tactical voting: in certain conditions, a voter's sincere ballot may not best defend their opinion.

Validated criteria for each method

Most data come from the comparison of electoral systems on Wikipedia. In some cases (marked with a ”?“) I don't know if the method validates the criterion.

	Condorcet	Majority	Monotonicity	Pareto efficiency	IIA	LIIA	Non-dictatorship	Strategy proof
Maximal lotteries
Randomized Condorcet
Ranked pairs
Schulze method
Kemeny–Young method
Minimax Condorcet method
Copeland's method
Approval voting
Borda's count
Instant-runoff
Coombs rule
Two-round system
Plurality
Random ballot

Related cool projects and stuff

You may want the check some related projects from other people:

Electoral system on Wikipedia.
To Build a Better Ballot: an interactive guide to alternative voting systems.
Politics in the animal kingdom: series of videos from CGP Grey (the great Youtuber) which presents voting methods.
Le scrutin de Condorcet randomisé: a Youtube video (in French) from the channel Science4All. The description contains many links to related work.
Handbook of Computational Social Choice: a 500 pager that can teach you everything about this topic.
Election Science - The center for election science: A non-partisan, non-profit dedicated to empowering people with voting methods that strengthen democracy. Their website is a wonderful source of content, for example, this interview of Dr Kenneth Arrow or this assessment of 6 single-winner voting methods.
fairvote.org: An initiative and application for Ranked Choice Voting (using Instant-run-off, or Single Transferable Vote in case of a multi-winner election). A voting application is also available on rankit.vote.
Modern Ballots: on-line and off-line voting platform using Schulze's method.
Condorcet Vote is a very similar application. It is written in PHP and the algorithms are available in a library
voting.ml: a voting tool originated from a project at the Technical University of Munich (TUM).
votation.ovh: an application (in French) to create votes using maximal lotteries.
votevote.page: an educational toy showing election results for many voting systems.